Variational Autoencoder

The objective of this project was to explore Variational Autoencoders (VAEs) using the Kuzushiji-MNIST dataset. The goal was simply to try it out for myself and see what kind of results I could get with KMNIST.

variational autoencoder

Variational Autoencoders make autoencoders into probabilistic models. Unlike standard autoencoders that learn deterministic encodings, VAEs impose a probabilistic structure on the latent space, which makes it possible to generate new samples by sampling from the learned distribution.

What this means is that the VAE training is based on maximizing the Evidence Lower BOund (ELBO), which provides a lower bound to the marginal log-likelihood $\log p(x)$:

$$\text{ELBO}(\theta, \phi; x) = E_{q_\phi(z|x)}[\log p_\theta(x|z)] - D_{KL}(q_\phi(z|x) || p(z))$$

Since we want to minimize a loss function during training, the VAE loss is the negative ELBO:

$$\mathcal{L}(\theta, \phi; x) = -\text{ELBO} = -E_{q_\phi(z|x)}[\log p_\theta(x|z)] + D_{KL}(q_\phi(z|x) || p(z))$$

Where:

• The first term is the reconstruction loss (negative log-likelihood)
• The second term is the KL divergence that regularizes the latent space
• $q_\phi(z|x)$ is the encoder (inference network)
• $p_\theta(x|z)$ is the decoder (generative network)

The encoder learns to map input data to a distribution in latent space:

$$q_\phi(z|x) = \mathcal{N}(\mu_\phi(x), \sigma_\phi^2(x))$$

While the decoder learns to reconstruct data from latent samples:

$$p_\theta(x|z) = \mathcal{N}(\mu_\theta(z), \sigma_\theta^2(z))$$

For an indepth explanaition of what all of that means you can take a look here From Autoencoder to Beta-VAE or An Introduction to Variational Autoencoders.

kuzushiji-mnist dataset

For this experiment, I used the Kuzushiji-MNIST dataset, which consists of 70,000 28x28 grayscale images of Japanese calligraphy characters. This dataset provides an interesting alternative to the standard MNIST digits, offering more complex character shapes and stroke patterns that make the learning task more challenging for generative models.

results

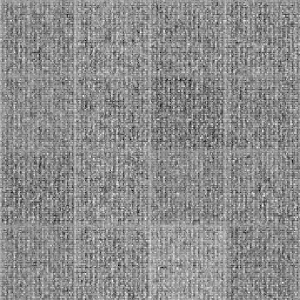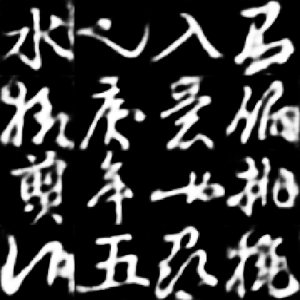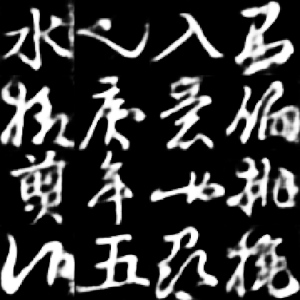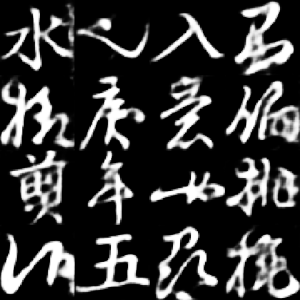
The first gif shows interpolation between encoded characters in the latent space after training was completed. By encoding real characters and then interpolating between their latent representations, we can observe how the VAE has organized the latent space and generates intermediate character forms.

The second gif displays random sampling from a grid of points in the latent space throughout the entire training procedure. This visualization shows how the model progressively learns to generate coherent character-like structures as training progresses.

The third gif demonstrates the reconstruction quality of specific selected characters during the training process. We can observe how the VAE gradually improves its ability to reconstruct the original characters, starting from noisy approximations and converging to cleaner, more accurate reconstructions.